⚙️ Two Pointers
투포인터 알고리즘(Two Pointers Algorithm) 또는 슬라이딩 윈도우(Sliding Window) 라고 부른다.
알고리즘 문제를 풀다 완전탐색으로 해결하면 시간 초과가 나는 문제가 종종 있는데, 이때 사용하면 빠르게 해결할 수 있다. 기본적인 원리는 다음과 같다.
1차원 배열이 있고, 이 배열에서 각자 다른 원소를 가리키고 있는 2개의 포인터를 조작해가면서 원하는 것을 얻기
N칸의 1차원 배열이 있을 때, 부분 배열 중 그 원소의 합이 M이 되는 경우의 수를 구한다고 생각해보자. 모든 경우의 수를 다 테스트 해보면 구간 합을 구간 배열로 O(1)만에 구한다고 해도 경우의 수는 O(N^2)이 된다. 따라서 문제를 풀 수 없다. N의 최대 범위가 너무 크기 때문이다. 그러나 이 경우 각 원소는 자연수이고 M 또한 자연수인데, 따라서 다음과 같이 풀 수 있다.
- 포인터 2개를 준비한다. 시작과 끝을 알 수 있도록 start, end 라고 한다.
- 맨 처음에는 start = end = 0이며, 항상 start<=end을 만족해야 한다.
- 2개의 포인터는 현재 부분 배열의 시작과 끝을 가리키는 역할을 한다.
s=e일 경우 그건 크기가 0인, 아무것도 포함하지 않는 부분 배열을 뜻한다. 다음의 과정을 s < N인 동안 반복한다.
- 만약 현재 부분합이 M 이상이거나, 이미 e = N이면 s++
- 그렇지 않다면 e++
- 현재 부분합이 M과 같으면 결과 ++
쉽게 이해하자면, start와 end 를 무조건 증가시키는 방향으로만 변화시켜가면서 도중에 부분 배열의 합이 정확히 M이 되는 경우를 세는 것이다.
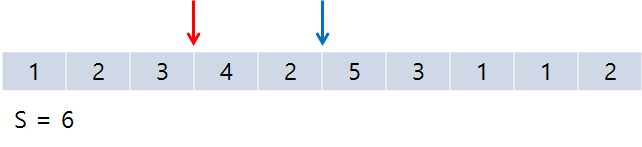
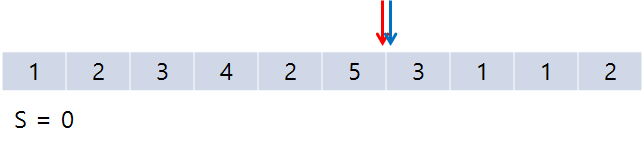
Ex) M = 5인 경우를 살펴보자.
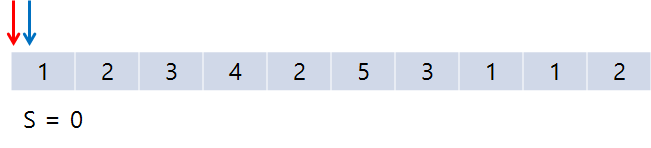
초기 상태이며, 빨간색 포인터 : start, 파란색 포인터 : end이다. S : 합.
end가 뒤로 움직일 때는 새로 포함한 원소를 S에 더하고, start가 뒤로 움직일 때는 새로 넘긴 원소를 S에서 빼는 식으로 현재 [start, end)의 합 S를 매번 쉽게 구할 수 있다.
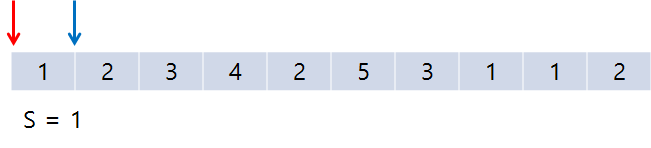
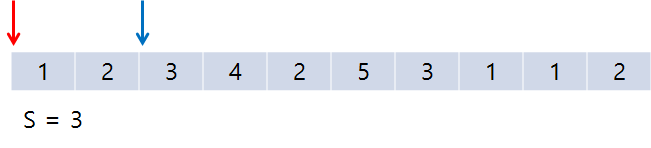
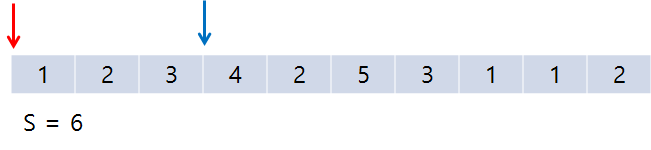
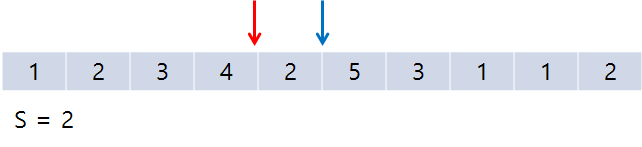
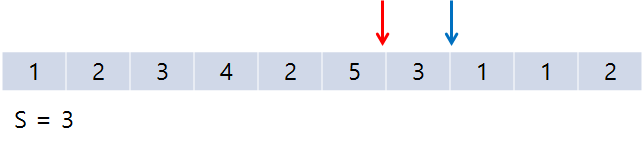
처음에는 이렇게 end만 증가하게 된다. S가 계속 M보다 작기 때문! 마지막엔 S>=M이 되었으므로 아래와 같다.
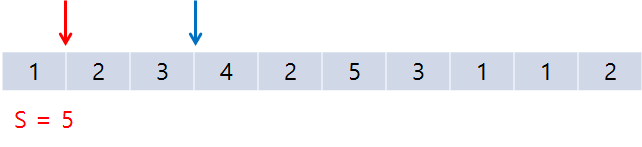
start를 한 칸 옮겼는데, 동시에 S = 5인 경우를 만났다. 이때 결과를 1 증가시켜 준다.
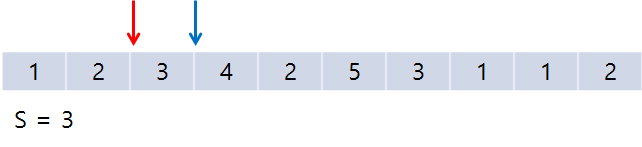
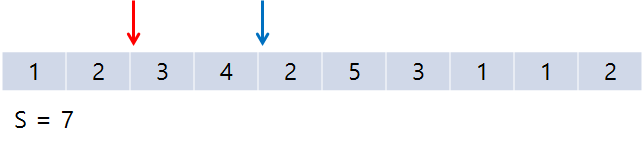
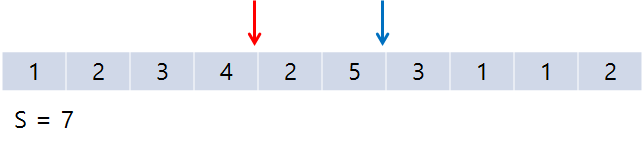
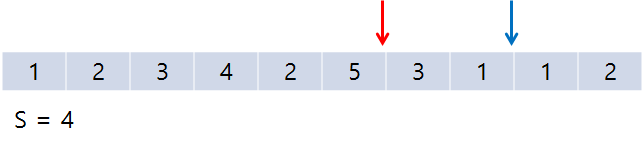
이런 식으로 포인터들이 움직이게 된다. 여기서 2번째로 S = 5인 지점을 만났으므로 결과를 1 증가시켜 준다.
그 직후, start가 1 증가하면서 start = end인 경우가 나온다.
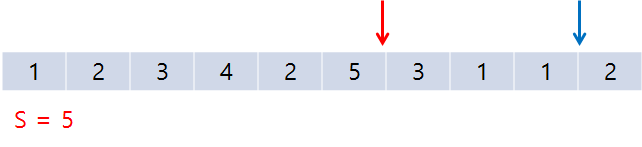
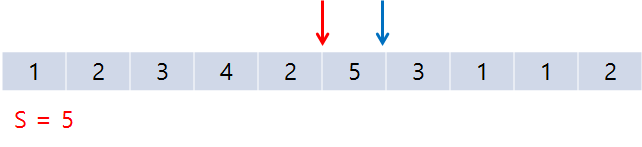
계속 가다 보면 세 번째로 S = 5인 지점을 만난다.
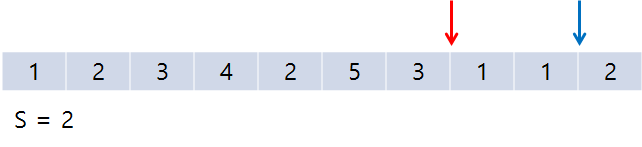
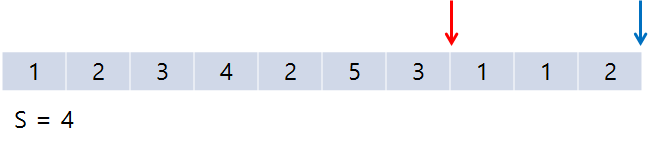
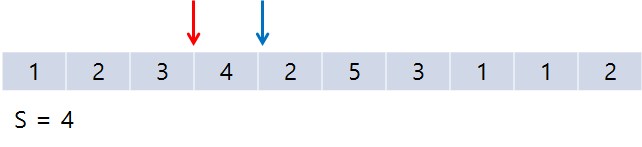
그 이후 조건에 맞춰 포인터를 증가시키다 보면, end가 배열 끝을 가리키게 되어 더이상 증가할 수 없는 상태가 된다.
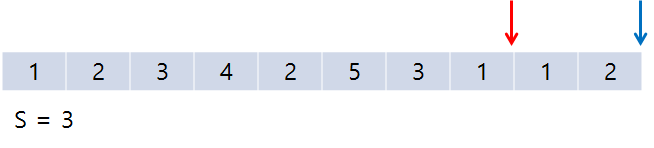
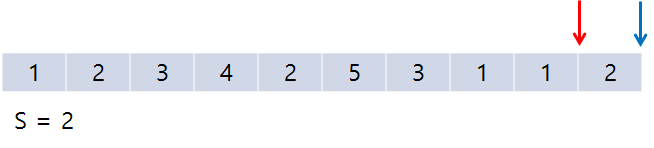
그렇게 되면 그냥 start만 증가시켜 가다가 start 역시 배열 끝에 다다르면 종료해도 되고, 그냥 그 자리에서 루프를 끝내버려도 된다. 이렇게 해서 S = 5인 경우는 3개 발견되었다.
시간 복잡도
- 이 알고리즘은 매 루프마다 항상 두 포인터 중 하나는 1씩 증가하고 있고, 각 포인터가 N번 누적 증가해야 알고리즘이 끝난다. 따라서 각각 배열 끝에 다다르는데
O(N)이라서 합쳐도O(N)이 된다.
- 이 알고리즘은 매 루프마다 항상 두 포인터 중 하나는 1씩 증가하고 있고, 각 포인터가 N번 누적 증가해야 알고리즘이 끝난다. 따라서 각각 배열 끝에 다다르는데
추천 문제(백준 기준)
- 2003 : 수들의 합
- 1644 : 소수의 연속합
- 1806 : 부분합
- 2230 : 수 고르기
- 1484 : 다이어트
- 2038 : 골룽 수열
- 2531 : 회전 초밥
- 2096 : 내려가기
- 2293 : 동전1