Gradient Descent Methods

Last updated Jan 19, 2023 Edit Source

• first-order(1차 미분한 값만 사용) interative(반복적으로)
• for finding a local minimum of a differentiable fuction.

• Generalization
  • 한 네트워크의 성능이 학습 데이터와 비슷하게 나올 것이라고 보장해줄 때.
• Under-fitting vs. over-fitting
  • 학습 데이터에 잘 동작하지만, 테스트 데이터에서 잘 동작하지 않을 때 Over-fitting이라고 한다.
  • 네트워크가 너무 간단하거나 해서 정답을 잘못 맞추는 것을 Under-fitting이라고 한다.
• Cross validation
  • 학습에 사용되지 않은 validation 데이터에 대해 얼마나 잘 동작하는지 보는 것.
  • Validation을 어느 크기로 해야 하는가?에 대한 답이 되는 개념.
  • 최적의 하이퍼 파라미터 셋을 찾고, 이후 제대로 학습할 때는 모든 데이터를 다 이용해서 학습시킨다.
  • 어느 경우에도 테스트 데이터셋을 사용하지 않는다!
• Bias-variance tradeoff
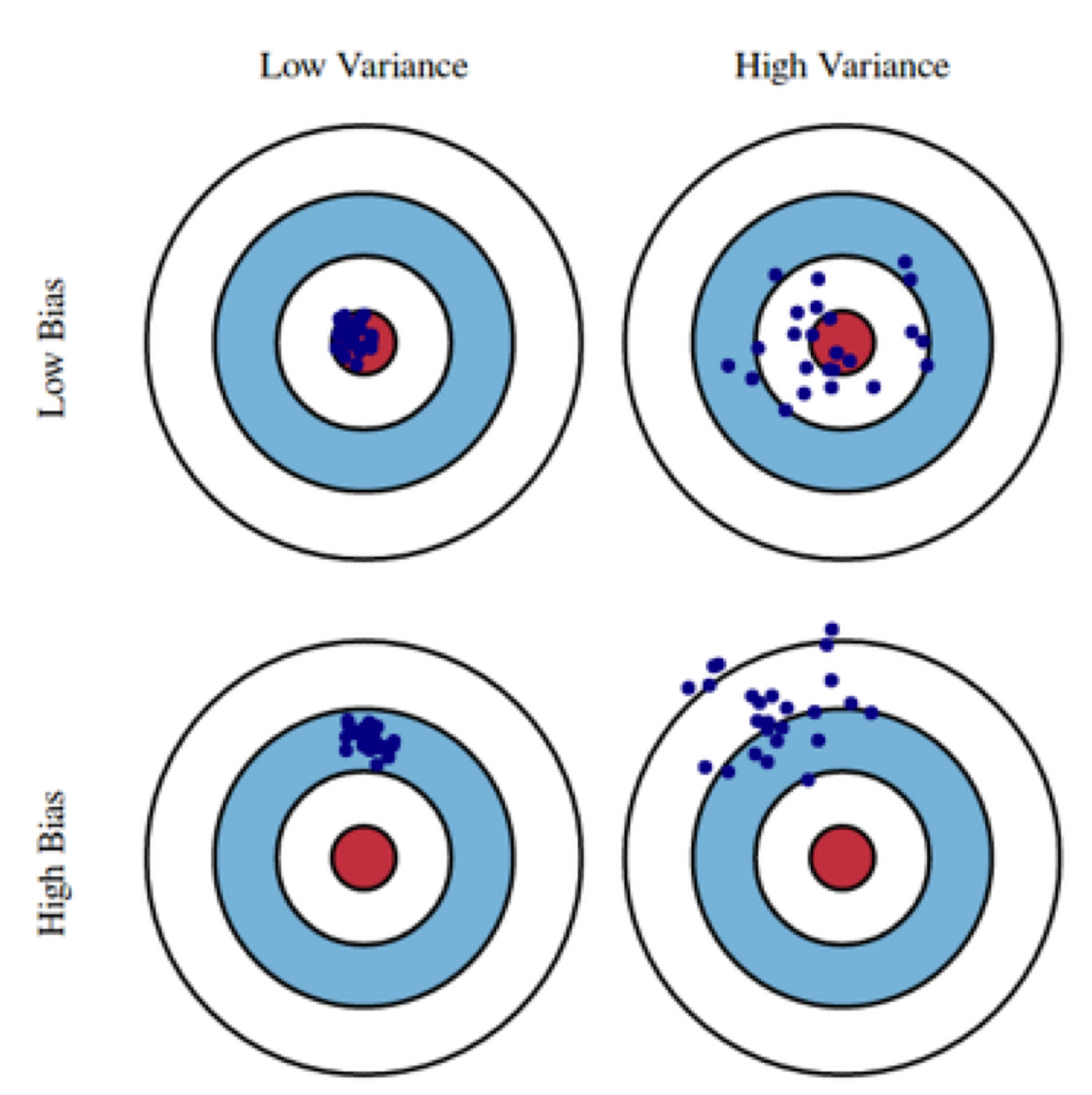
  • Variance: 출력이 얼마나 일관되는가? Variance가 클수록 출력이 분산되어 있다.
  • Bias: 평균적으로 봤을 때, True target에 가까이 있는가? Bias가 높을 수록 True target에서 떨어져 있는 것이다.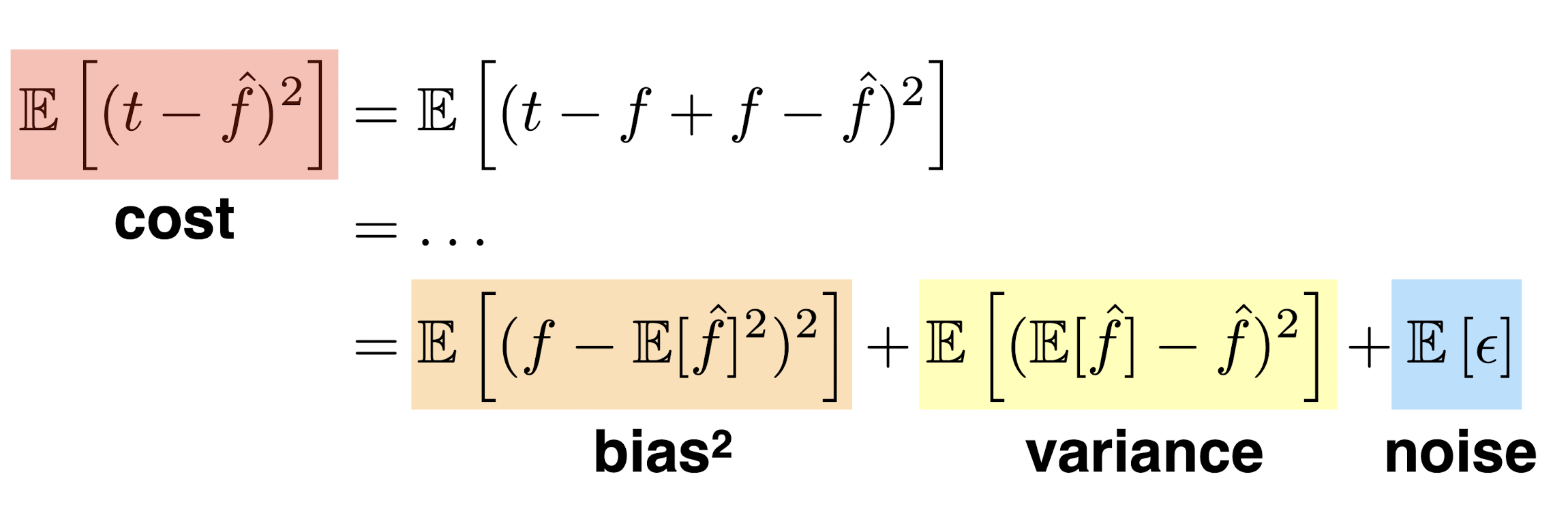
  • 이 둘은 Tradeoff 관계에 있다. 이 둘을 모두 동시에 줄이는 것은 어렵다.
• Bootstrapping
  • 서브 샘플링을 통해 여러 데이터셋, 여러 모델을 만들고 하겠다는 방법.
• Bagging and boosting
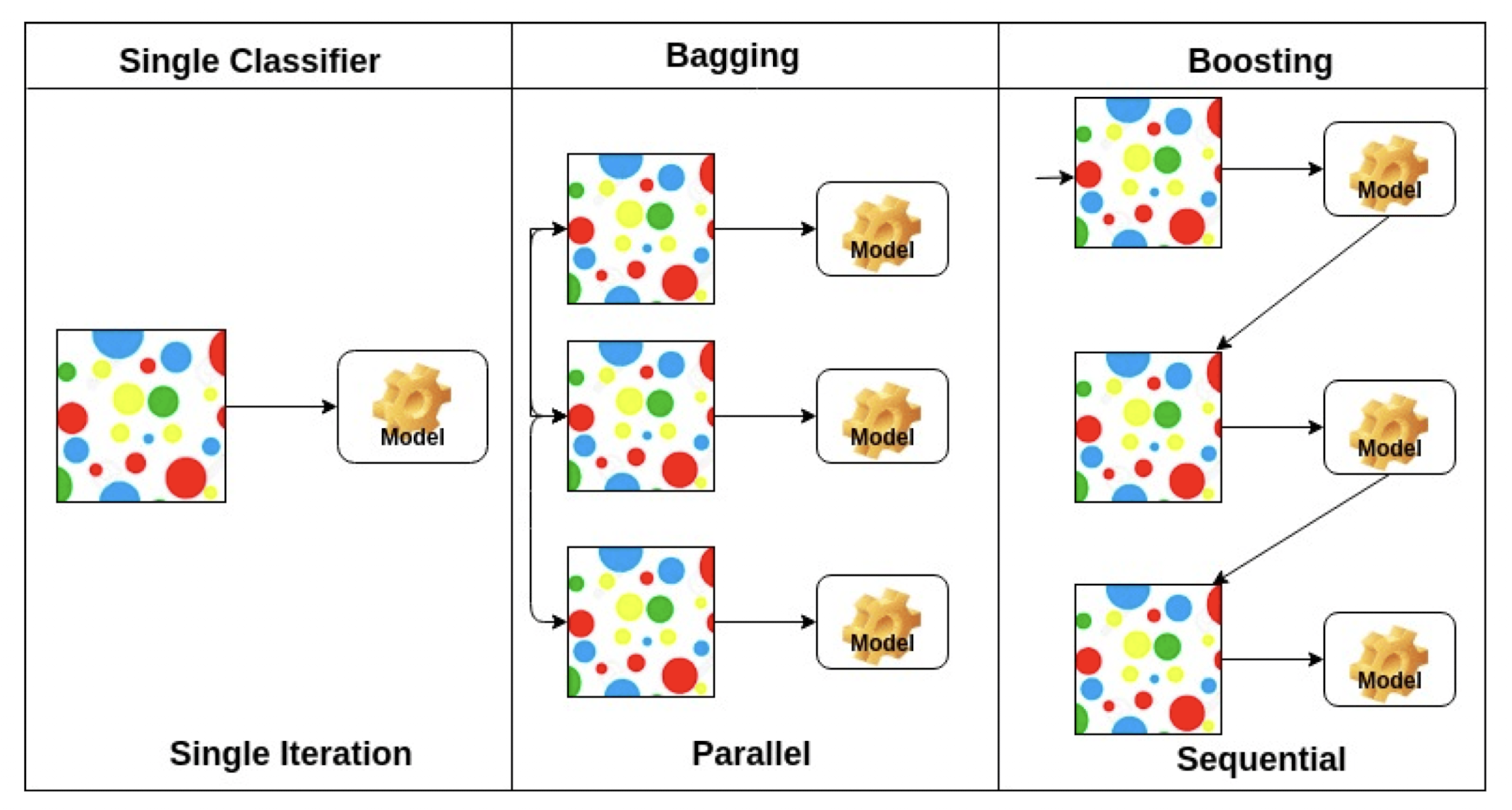
  • Bagging :부트스트래핑으로 여러 모델을 만들고 그들의 출력을 평균내겠다는 방법.
    • ex) ensemble 기법
  • Boosting: 모델을 만들고, 그 모델(weak learner)이 잘 못하는 것에 대해서만 모델을 만들고, 만들고… 쭉 해서 이들을 시퀀셜하게 합쳐서 하나의 strong learner를 만드는 것. 결과적으로 하나의 모델이 만들어진다.

1. SGD
   1. 한 개(single sample)만 보고 업데이트, 한 개만 보고 업데이트 …
2. Mini-batch gradient descent
   1. 배치 사이즈마다 업데이트 → 일반적인 방법임.
3. Batch gradient descent
   1. 한 번에 다 보고 업데이트

배치 사이즈는 중요하다.

• 큰 배치 사이즈를 사용하면 sharp minimizers에 도달한다.
• 작은 배치 사이즈를 사용하면 flat minimizers에 도달한다.
• sharp 보다는 flat이 좋다. 왜?
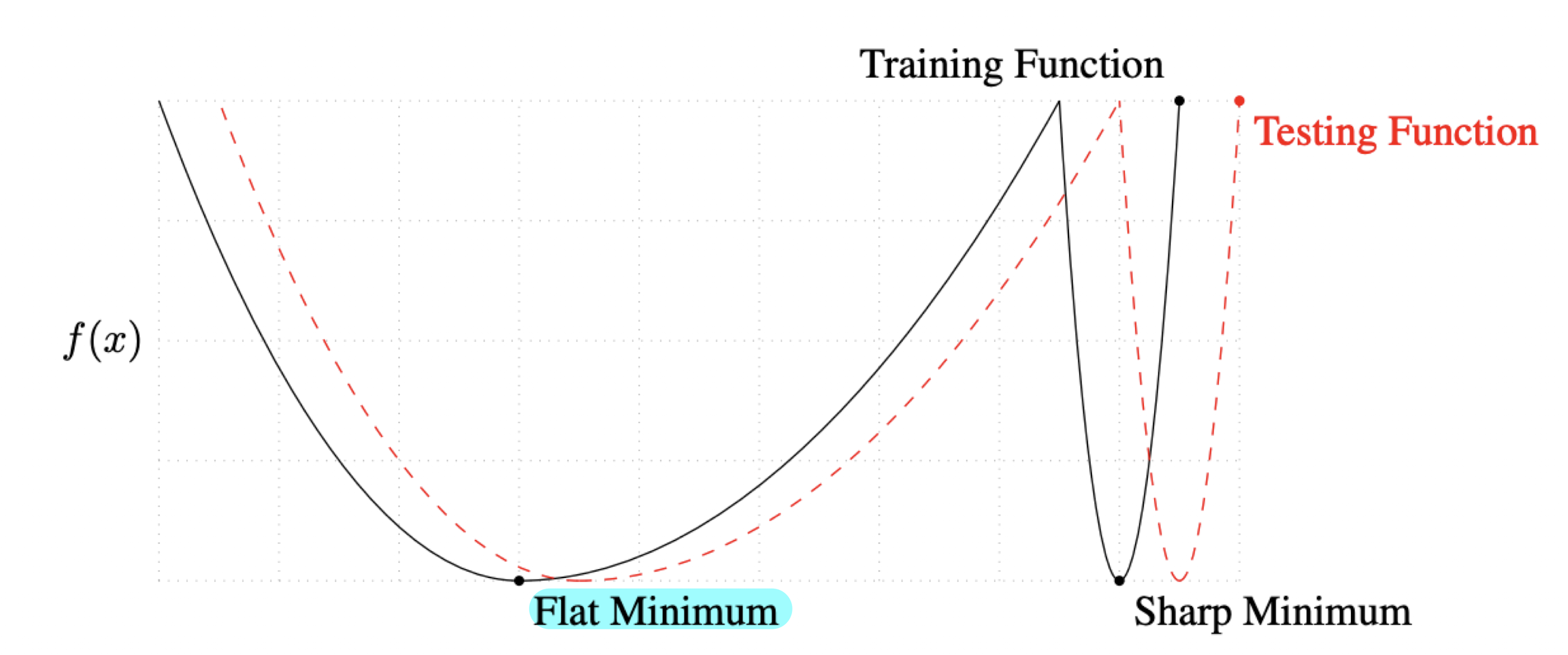
• Flat minimizers는 좀 떨어져도 어느 정도 작은 값을 보장한다.
• 반면, Sharp minimizers는 조금만 떨어져도 높게 되어버려 일반화 성능이 떨어진다.
• 작은 배치 사이즈가 일반화에 더 좋다.

• Gradient Descent:
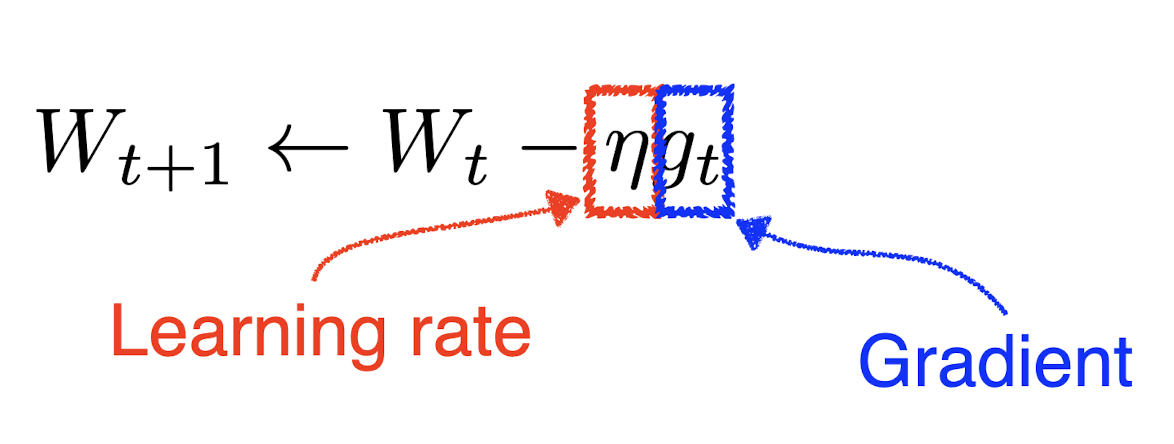
  • 러닝 레이트 잡기가 어렵다. 더 빨리 학습시키는 방법은 없을까?
  • → 여러 최적화 테크닉들이 출현.
• Momentum: 이전 배치에서 흐른 정보를 활용하자.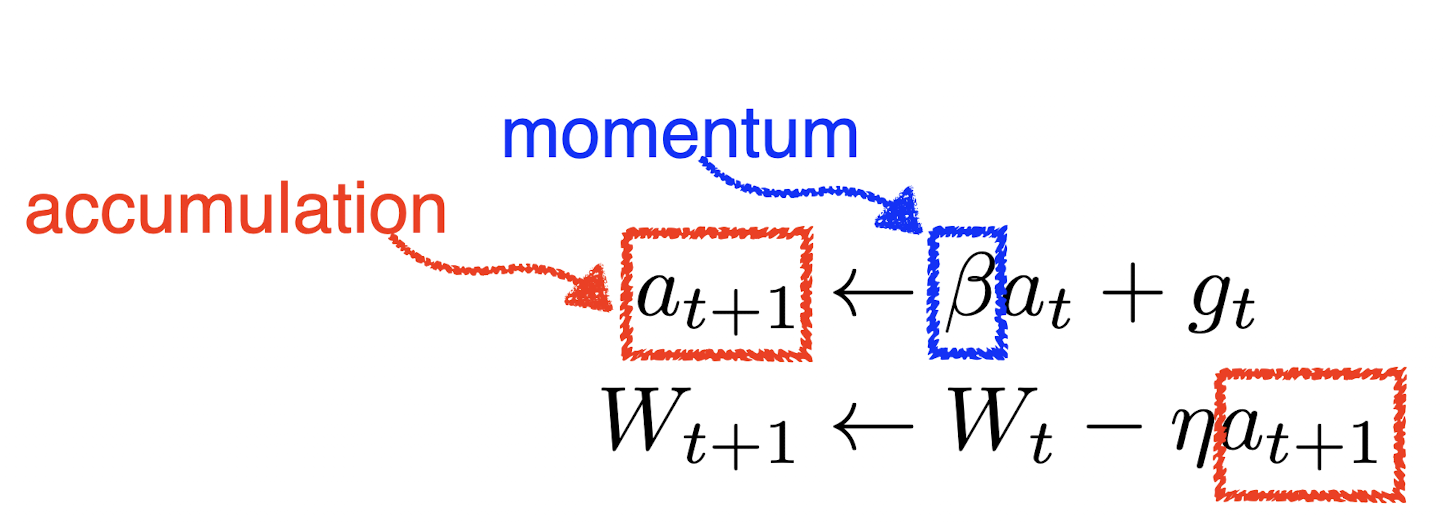
  • 한 번 흘러가기 시작한 흐름을 어느 정도 유지시켜준다. 그레디언트가 왔다갔다 해도 어느 정도는 잘 학습시켜준다는 장점.
• NAG: 모멘텀에다가 Lookahead gradient를 사용하여, 한 번 이동하게 된다.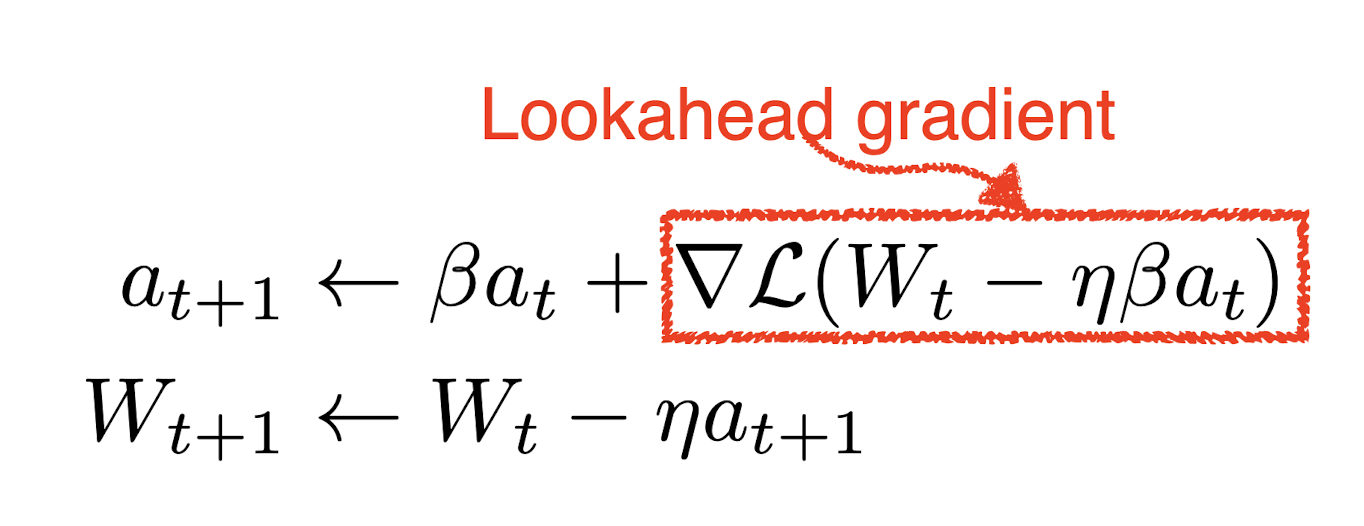
  • local minimum을 지나지 않고 그 아래로 빨리 컨버징한다는 장점.
• Adagrad: 지금까지 변한 그레디언트($G_t)$에 따라서 조정.
  • 많이 변한 그레디언트는 적게 변화시키고, 적게 변화시킨 그레디언트는 크게 변화시킨다.
  • $G_t$가 무한대로 커지면, 즉, 뒤로 가면 갈 수록 학습이 멈춰지게 된다는 단점 존재.
• Adadelta: $G_t$가 계속 커지는 것을 어느 정도 막겠다. EMA 사용
  • $H_t$라는 새로운 파라미터가 추가됨.
  • 러닝 레이트가 사용되지 않음.
• RMSprop: EMA 사용, 강의 때 교수가 제안
• Adam : 그레디언트 조정과 모멘텀을 둘 다 쓰겠다는 아이디어.
  • $\beta_1, \beta_2$ 파라미터를 사용한다.
  • 0으로 나눠지는 것을 막기 위해 $\epsilon$ (epsilon)도 사용하는데 이 파라미터도 아주 중요!