Neural Language Generation

Last updated Mar 14, 2023 Edit Source

What is natural language generation?
Any task involving text production for human consumption requires natural language generation.

• 자연어 생성의 기초

  • In autoregressive text generation models, at each time step $t$, our model takes in a sequence of tokens of text as input ${y}_{<t}$ and outputs a new token, ${\hat{y}}_t$.
  • 
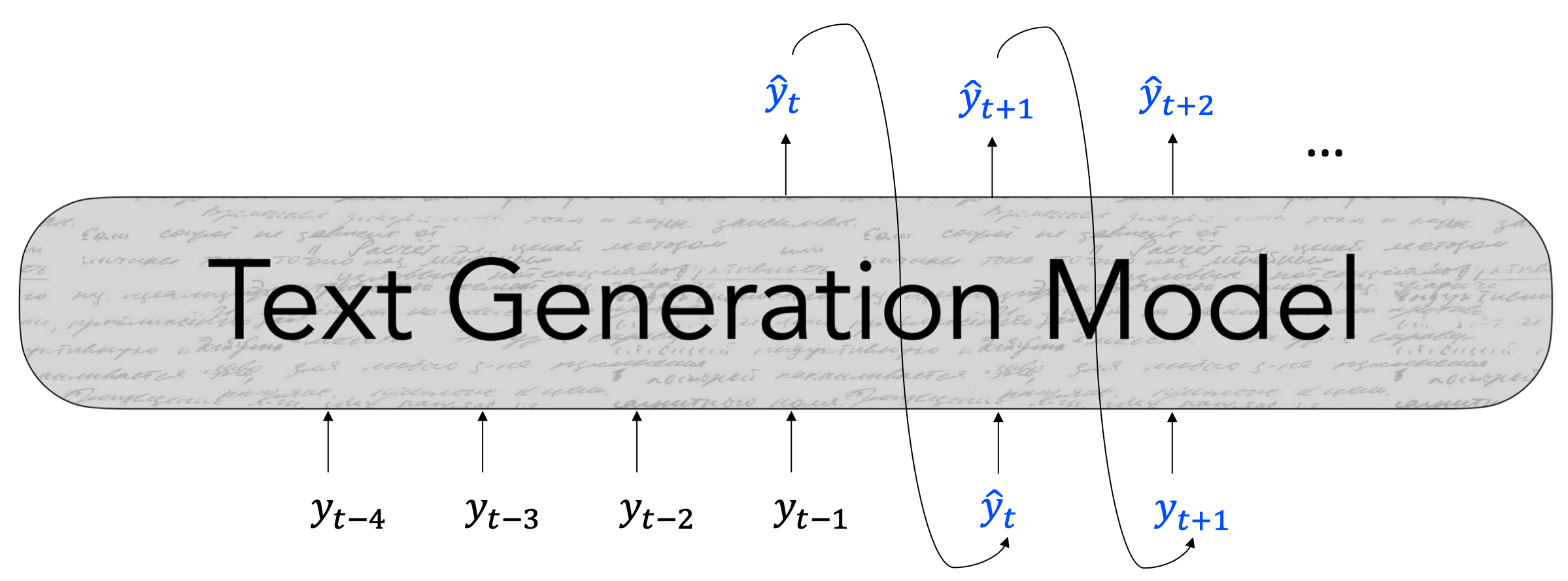
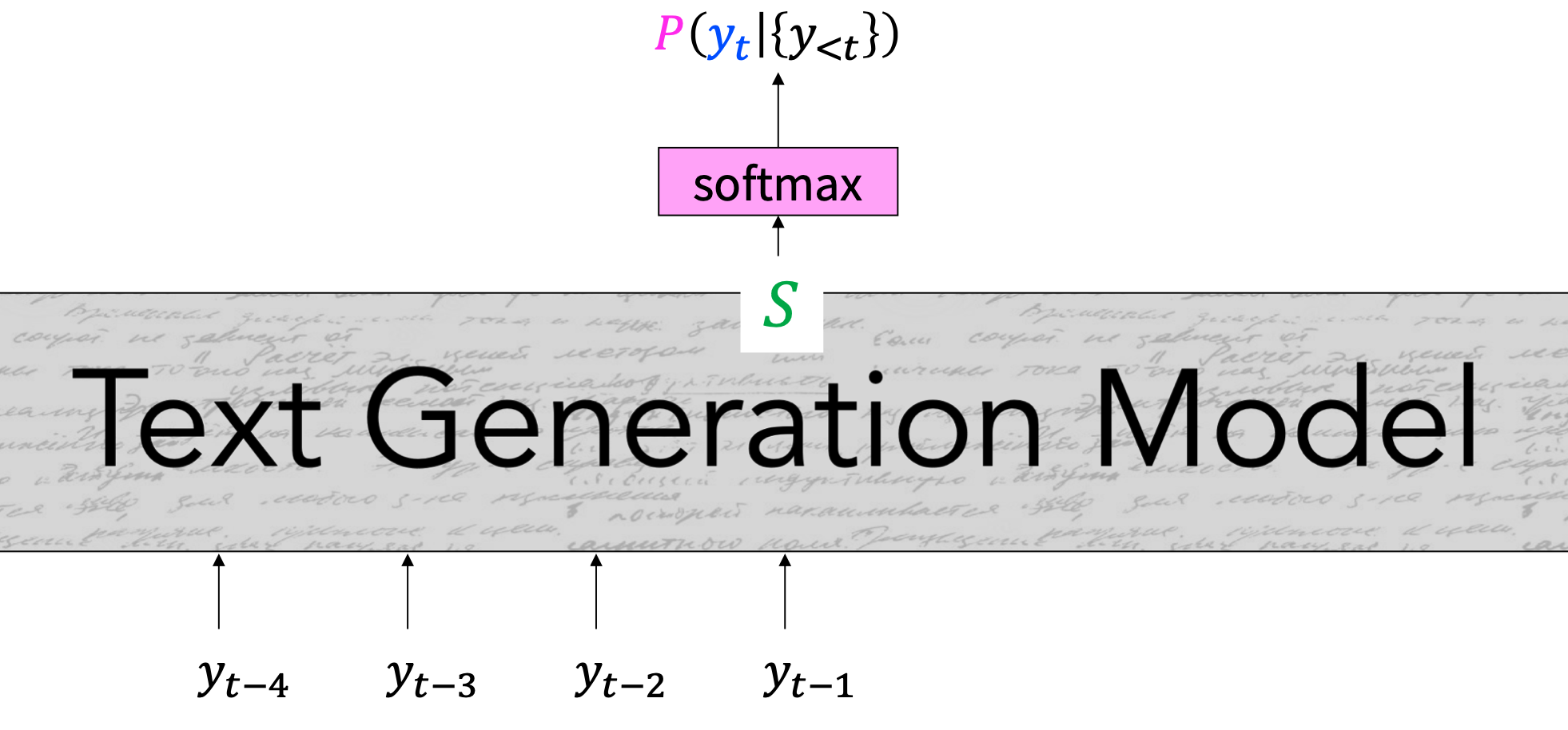
  • At each time step $t$, our model computes a vector of scores for each token in our vocabulary, $S \in \mathbb{R}^V$: $$S = f({y_{<t}}, \theta)$$
  • Then, we compute a probability distribution $𝑃$ over $w \in V$ using these scores: $$P(y_t = w | {y_{<t}}) = {{exp(S_w)} \over {\sum_{w’\in V} exp(S_{w’})}}$$

• What are we trying to do?

  • At each time step $t$, our model computes a vector of scores for each token in our vocabulary, $S \in \mathbb{R}^V$). Then, we compute a probability distribution $P$ over $w \in V$ using these scores:
  • At inference time, our decoding algorithm defines a function to select a token from this distribution: $${\hat{y_t}} = g(P(y_t|{y_{<t}})$$
    • In the equation above, $\color{red}g(\cdot)$ is your decoding algorithm.
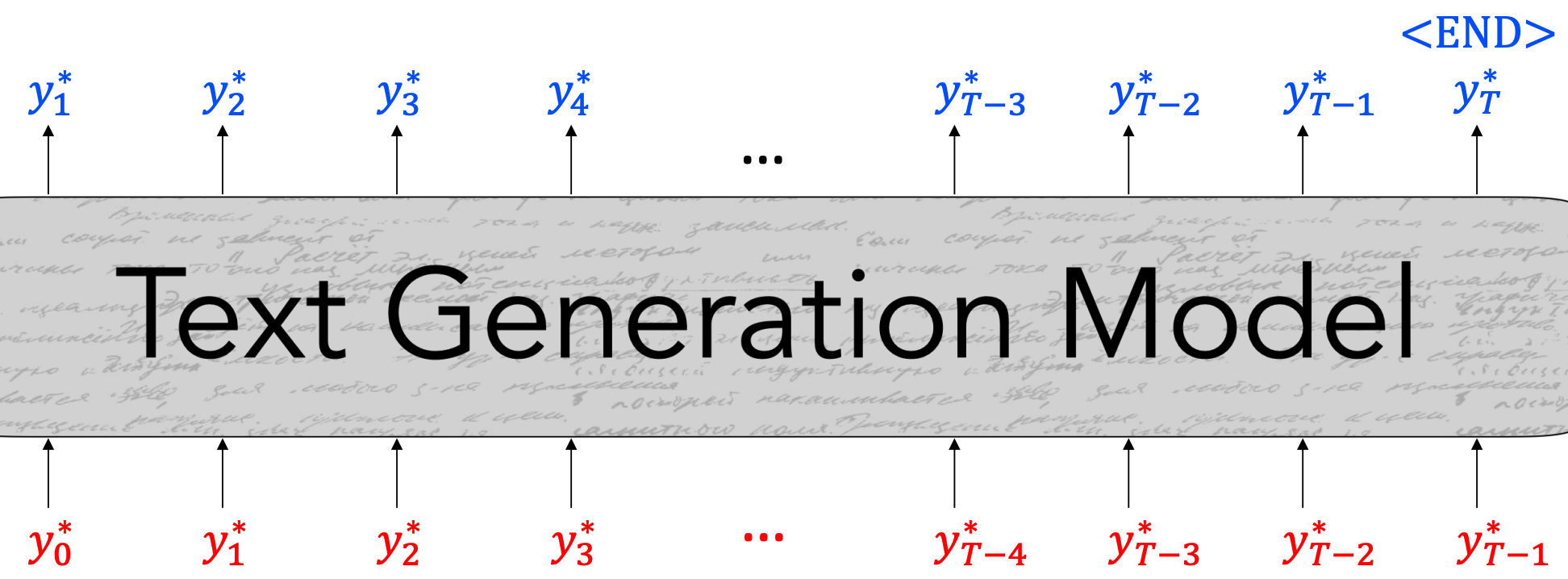
    • We train the model to minimize the Negative loglikelihood of predicting the next token in the sequence: $$L_t = -logP(y_t^* | {y_{<t}^*})$$
  • The label at each step is the actual word $\color{blue}y_t^*$ in the training sequence.
  • This token is often called the “gold” or “ground truth” token.
  • 이러한 알고리즘을 “teacher forcing”이라고 한다.

• Maximum Likelihood Training (i.e., Teacher forcing)

  • Trained to generate the next word $\color{blue}y_t^$ given a set of preceding words $\color{red}{y_{<t}^}$.
  • 모델의 출력값이 다음 타임 스텝에 입력값으로 들어가는 방식. $$L = -\sum_{t=1} logP({\color{blue}y_t^} | {\color{red}{y_{<t}^}})$$

• Our decoding algorithm defines a function to select a token from this distribution: $${\hat{y_t}} = {\color{blue}g}(P(y_t|{y_{<t}})$$
• 여기서 $g(\cdot)$ 이 decoding 알고리즘이다.
• Greedy methods
  • Argmax Decoding
    • Selects the highest probability token in $P(y_t|y_{<t})$ $${\hat{y_t}} = {\color{red}argmax_{w \in V}}P(y_t = w | y_{<t})$$
  • Beam Search
    • Also a greedy algorithm, but with wider search over candidate
  • 그러나 Greedy methods는 repetitive 위험이 높다.
  • 어떻게 repetition을 줄일 수 있을까?
    • Simple option: “Don’t repeat n-grams”
    • More complex:
      • Minimize embedding distance between consecutive sentences (Celikyilmaz et al., 2018)
      • Coverage loss (See et al., 2017)
      • Unlikelihood objective (Welleck et al., 2020)
• ==Decoding: Top-k sampling==
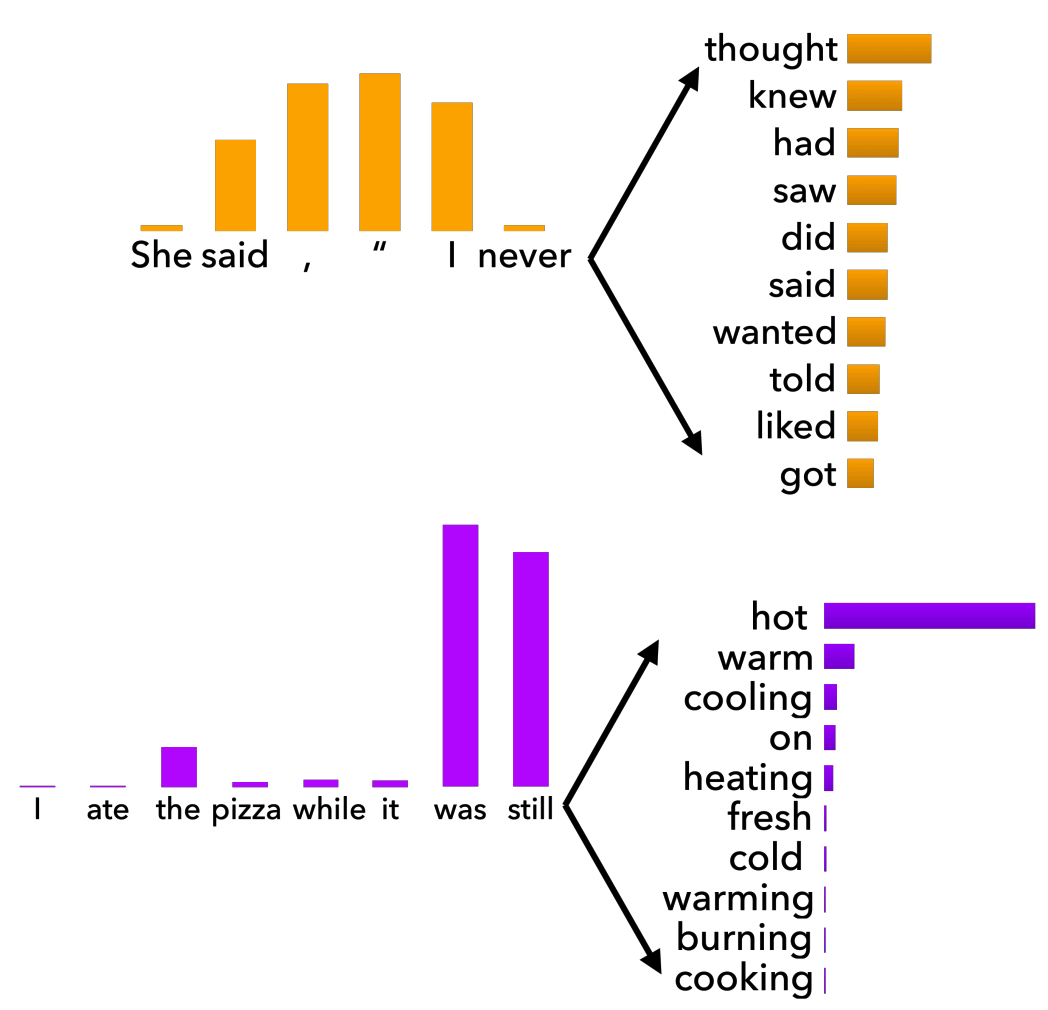
  • Problem: Vanilla sampling makes every token in the vocabulary an option
    • Even if most of the probability mass in the distribution is over a limited set of options, the tail of the distribution could be very long
    • Many tokens are probably irrelevant in the current context
    • Why are we giving them individually a tiny chance to be selected?
    • Why are we giving them as a group a high chance to be selected?
  • Solution: Top-k sampling
    • Only sample from the top k tokens in the probability distribution.
    • Increase k for more diverse/risky outputs
    • Decrease k for more generic/safe outputs
    • Top-k sampling can cut off too quickly!
      • 각 토큰이 비슷한 확률 분포를 가지면 빠르게 cut-off 한다.
    • Top-k sampling can also cut off too slowly!
      • 그러나, 소수의 토큰이 높은 확률을 갖고 나머지가 아주 낮은 확률을 갖는다면, 상당히 느리게 cut-off 할 것이다.
• ==Decoding: Top-p sampling==
  • 등장 배경: The probability distributions we sample from are dynamic.
    • When the distribution $P_t$ is flatter, a limited $k$ removes many viable options.
    • When the distribution $P_t$ is peakier, a high $k$ allows for too many options to have a chance of being selecte.
  • 이 문제를 해결할 방법: Top-p sampling
    • Sample from all tokens in the top $p$ cumulative probability mass (i.e., where mass is concentrated).
    • Varies k depending on the uniformity of $P_t$.
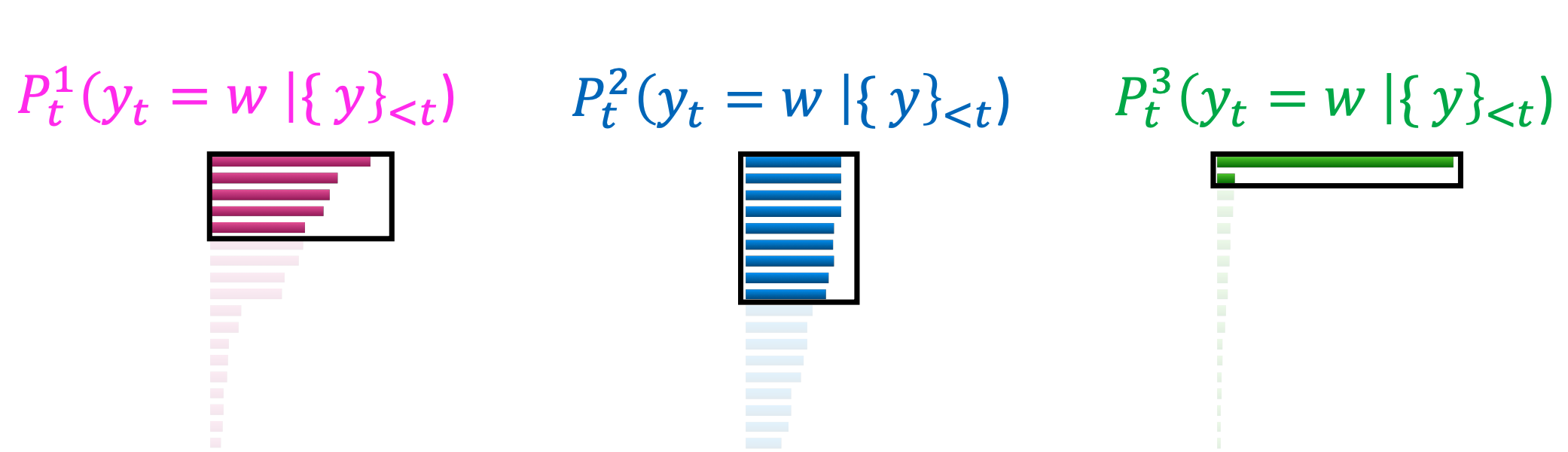
  • Scaling randomness: == Softmax temperature==
    • You can apply a temperature hyperparameter $\tau$ to the softmax to rebalance $P_t$! $$P_t(y_t = w) = {{exp({\color{blue}S_w / \tau})} \over {\sum_{w’\in V} exp({\color{blue}S_{w’/ \tau}})}}$$
    • Raise the temperature $\tau$ > 1: $P_t$ becomes more uniform
      • More diverse output (probability is spread around vocab)
    • Lower the temperature $\tau$ < 1: $P_t$ becomes more spiky
      • Less diverse output (probability is concentrated on top words

Note

Softmax temperature is not a decoding algorithm! It’s a technique you can apply at test time, in conjunction with a decoding algorithm (such as beam search or sampling)

Decoding: Takeaways

• Decoding is still a challenging problem in natural language generation
• Human language distribution is noisy and doesn’t reflect simple properties (i.e., probability maximization)
• Different decoding algorithms can allow us to inject biases that encourage different properties of coherent natural language generation
• Some of the most impactful advances in NLG of the last few years have come from simple, but effective, modifications to decoding algorithms

• Maximum Likelihood Training (i.e., teacher forcing)
  • Trained to generate the next word $\color{blue}y_t^$ given a set of preceding words $\color{red}{y_{<t}^}$.
  • Diversity Issues
    • Maximum Likelihood Estimation discourages diverse text generation.
• Unlikelihood training
  • Given a set of undesired tokens $C$, lower their likelihood in context. $$L_{UL}^t = -\sum_{y_{neg} \in C} log(1-P(y_{neg} | {y^*}_{<t}))$$
  • Keep teacher forcing objective and combine them for final loss function. $$L_{MLE}^t = -\sum_{t=1} logP(y_t^* | {y^*}{<t})$$ $$L{ULE}^t = L_{MLE}^t + aL_{UL}^t$$
  • Set $C = {y^*}_{<t}$ and you’ll train the model to lower the likelihood of previously-seen tokens!
    • Limits repetition!
    • Increases the diversity of the text you learn to generate.
• == Exposure bias==
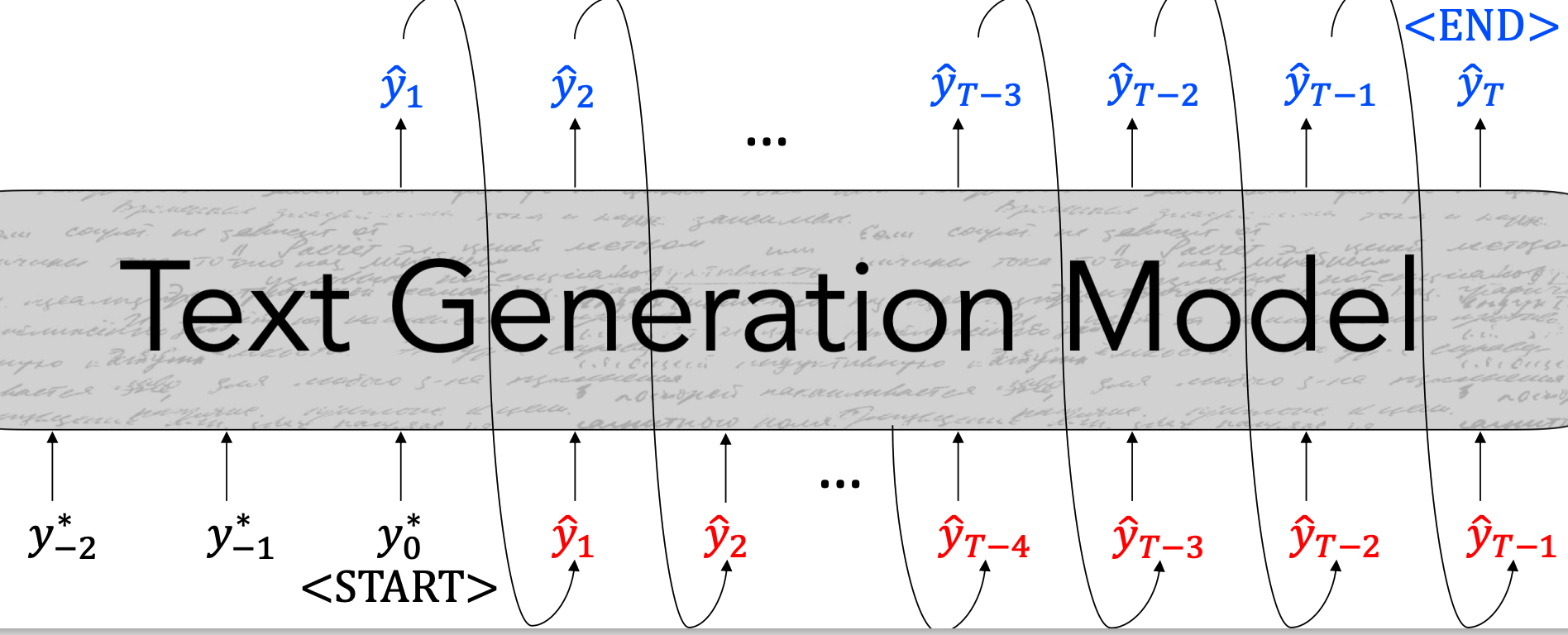
  • Training with teacher forcing leads to exposure bias at generation time
  • During training, our model’s inputs are gold context tokens from real, human-generated texts. $$L_{MLE} = -logP(y_t^* | {\color{red}{y^*}_{<t}})$$
    • At generation time, our model’s inputs are previously–decoded tokens. $$L_{dec} = -logP(\hat{y}t | {\color{blue}\hat{y}{<t}})$$
  • Exposure Bias Solutions
    • Scheduled sampling (Bengio et al., 2015)
    • Dataset Aggregation (DAgger; Ross et al., 2011)
    • Sequence re-writing (Guu*, Hashimoto* et al., 2018)
    • Reinforcement Learning: cast your text generation model as a Markov decision process
      • State $s$ is the model’s representation of the preceding context
      • Actions $a$ are the words that can be generated
      • Policy $\pi$ is the decoder
      • Rewards $r$ are provided by an external score
      • Learn behaviors by rewarding the model when it exhibits them.
      • REINFORCE: Basic
        • Sample a sequence from your model
        • Next time, increase the probability of this sampled token in the same context.
        • …but do it more if I get a high reward from the reward function. $$L_{RL} = -\sum_{t=1}^T {\color{red}r(\hat{y_t})}logP(\hat{y}t | y^*;{\color{blue}{\hat{y_t}}{<t}})$$
        • Reward Estimation
          • How should we define a reward function? Just use your evaluation metric!
          • BLEU (machine translation; Ranzato et al., ICLR 2016; Wu et al., 2016)
          • ROUGE (summarization; Paulus et al., ICLR 2018; Celikyilmaz et al., NAACL 2018)
          • CIDEr (image captioning; Rennie et al., CVPR 2017)
          • SPIDEr (image captioning; Liu et al., ICCV 2017)
        • The dark side…
          • Need to pretrain a model with teacher forcing before doing RL training
            • Your reward function probably expects coherent language inputs…
          • Need to set an appropriate baseline $$L_{RL} = -\sum_{t=1}^T {\color{red}r(\hat{y_t} - b)}logP(\cdots)$$
          • Use linear regression to predict it from the state $s$ (Ranzato et al., 2015)
          • Decode a second sequence and use its reward as the baseline (Rennie et al., 2017)

Training: Takeaways

• Teacher forcing is still the premier algorithm for training text generation models
• Diversity is an issue with sequences generated from teacher forced models
  • New approaches focus on mitigating the effects of common words
• Exposure bias causes text generation models to lose coherence easily
  • Models must learn to recover from their own bad samples (e.g., scheduled sampling, DAgger)
  • Or not be allowed to generate bad text to begin with (e.g., retrieval + generation)
• Training with RL can allow models to learn behaviors that are challenging to formalize
  • Learning can be very unstable.

Evaluating NLG systems

• Types of evaluation methods for text generation
  • Content overlap metrics
  • Model-based Metrics
  • Human Evaluations
• Content overlap metrics
  • Compute a score that indicates the similarity between generated and gold-standard (human-written) text
  • Fast and efficient and widely used
  • Two broad categories:
    • N-gram overlap metrics (e.g., BLEU, ROUGE, METEOR, CIDEr, etc.)
      • They’re not ideal for machine translation.
    • Semantic overlap metrics (e.g., PYRAMID, SPICE, SPIDEr, etc.
• Model-based metrics
  • Use learned representations of words and sentences to compute semantic similarity between generated and reference texts.
  • No more n-gram bottleneck because text units are represented as embeddings!
  • Even though embeddings are pretrained, distance metrics used to measure the similarity can be fixed.
  • Model-based metrics: Word distance functions
    • Vector Similarity
      • Embedding Average (Liu et al., 2016)
      • Vector Extrema (Liu et al., 2016)
      • MEANT (Lo, 2017)
      • YISI (Lo, 2019)
    • Word Mover’s Distance
    • BERT SCORE
      • Uses pre-trained contextual embeddings from BERT and matches words in candidate and reference sentences by cosine similarity. (Zhang et.al. 2020)
  • Model-based metrics: Beyond word matching
    • Sentence Movers Similarity
    • BLEURT
      • A regression model based on BERT returns a score that indicates to what extend the candidate text is grammatical and conveys the meaning of the reference text. (Sellam et.al. 2020)
• Human evaluations
  • Most important form of evaluation for text generation systems
  • Ask humans to evaluate the quality of generated text

Note

Don’t compare human evaluation scores across differently-conducted studies. Even if they claim to evaluate the same dimensions!

• Learning from human feedback
  • ADEM
  • HUSE

Evaluation: Takeaways

• Content overlap metrics provide a good starting point for evaluating the quality of generated text, but they’re not good enough on their own.
• Model-based metrics are can be more correlated with human judgment, but behavior is not interpretable.
• Human judgments are critical.
  • Only ones that can directly evaluate factuality – is the model saying correct things?
  • But humans are inconsistent!
• In many cases, the best judge of output quality is YOU!