선형독립과 선형종속

Last updated Jan 9, 2023 Edit Source

$R_n$ 공간에서 vector $\left { v_1, \cdots, v_p \right }$ 가 있을 때 만약 벡터 방정식이 trivial solution(자명해)만 갖고 있을 시에 선형 독립이라고 한다. 즉, trivial solution만 있으면 linearly independent이다. trivial solution만 존재한다는 의미는 free variable이 없다는 의미이다.

벡터 방정식 $c_1v_1+…+c_pv_p=0$에서 weight c1,…,cp 중 하나라도 non zero면 선형 종속이라고 한다. nontrivial solution을 갖고 있으면 최소 1개가 nonzero, 여러개가 zero 일 수 있으므로 linear combination으로 표현되지 않을 수 있다.

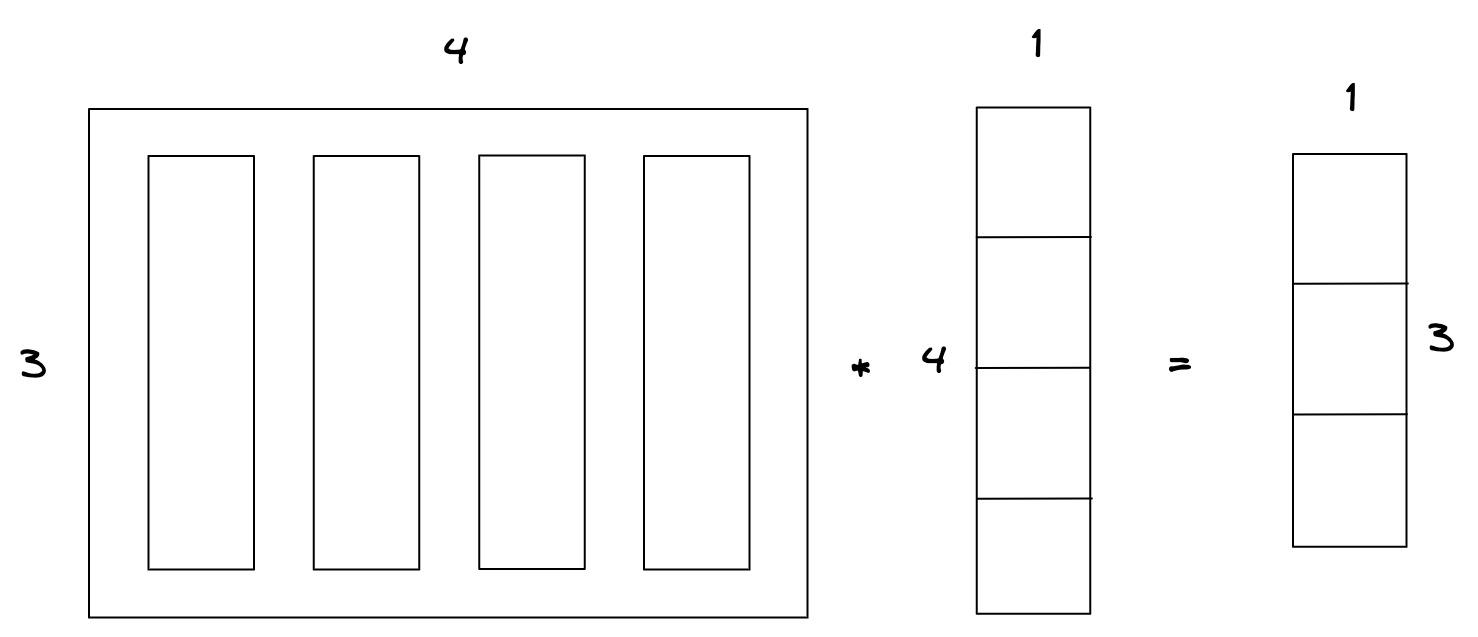
위 그림은 열벡터(재료벡터, an) * 가중치(xn)의 선형결합으로 표현될 수 있는데, 이때 재료벡터의 차원수(3)보다 미지수 갯수(xn= 4)가 더 많으므로, 해가 무수히 많게 된다.

반대로,

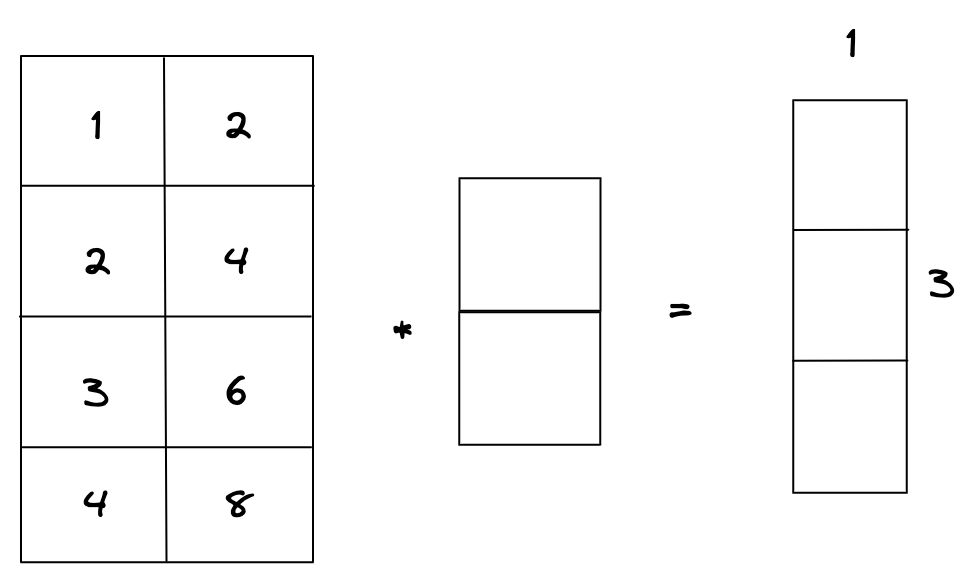
이 그림은 재료벡터의 차원수(4)가 미지수 개수(xn = 2)보다 많은데, 이 경우에는 없거나 무수히 많게 된다. 즉, 케이스 바이 케이스이다. 언제 해가 없냐면, 위 그림처럼 두 재료벡터의 원소가 서로의 배수일 경우이다. 이러면 스팬이 평행사변형을 이루지 못하고 선형이 되기 때문에, 서로 선형종속이 되어버려 해가 존재하지 않게 된다.

마지막으로, 재료벡터의 차원 수와 미지수 개수가 같다면,

• 재료 벡터끼리 선형 독립이면, 해가 하나이다.
• 재료 벡터끼리 선형 종속이면, 해가 무수히 많다.