Span & Basis
# Span(생성)
# 기저와 차원(Basis, Dimension)
$\vec{v}_1, \vec{v}_2,…, \vec{v}_r$의 linear combination으로 만들 수 있는 모든 vector들의 집합을 set spanned by $\vec{v}_1, \vec{v}_2, \cdots, \vec{v}_r$이라고 부르고
$$\mathrm{span}(\left {\vec{v}_1,\vec{v}_2,\cdots,\vec{v}_r \right })$$
이라고 표현한다. (이 집합은 기존 vector space의 부분 집합이면서 동시에 그 자신이 vector space가 되는데 이러한 경우, 이 집합을 기존 vector space의 subspace라고 부른다.)
# Basis of Vector Space
거의 대부분 vector space들은 무한히 많은 vector들을 가지고 있기 때문에 이들 전부를 각각 다루기보다는 적당히 대표적인 vector들을 이용하여 모든 vector에 대한 분석을 할 수 있으면 좋을 것이다. 이러한 vector들은 vector space 전체를 표현할 수 있어야 하므로,
- 모든 vector들은 대표적인 vector들의 linear combination으로 나타낼 수 있어야 하고 (spanned set이 vector space 전체가 되어야 하고)
최대한 적은 수의 vector들로 표현하는 것이 유리할 것이므로 linearly dependent한 vector들은 linearly independent한 vector들만 남겨놓는다면,
- 서로 linearly independent 해야 한다.
이러한 두 가지 조건을 만족하는 vector들의 집합을 basis라고 부른다.
DEFINITION: Basis of Vector Space
Vector space V의 부분 집합 B가
- $span(B)=V$
- B의 vector들은 서로 linearly independent
하면 B를 V의 basis라고 부른다.
Basis를 구성하는 vector의 수보다 많은 수의 vector들은 linearly dependent이다. 예를 들어, basis가 $$ { \vec{e}_1, \vec{e}_2, \cdots , \vec{e}_n } $$ 이라면, vector $\vec{v}_1,\vec{v}_2,\cdots,\vec{v}_n$ 은 각각이 basis vector의 linear combination
$$\vec{v}i= \sum{j=1}^n a_{ij} \vec{e}_j$$
로 표현되고, 만약
$$\vec{0}= \sum_{i=1}^{n+1} x_i \vec{v_i} = \sum_{i=1}^{n+1} \sum_{j=1}^n x_i a_{ij} \vec{e_j} $$ 이라면 basis의 정의에 따라,
$$ \sum_{i=1}^{n+1} a_{ij} x_i =0 $$
이어야 하는데,
이것은 미지수는 n+1개 이지만, 식은 n개 밖에 없는 연립방정식이다. 그러므로 이 연립방정식의 해는 없거나 무한히 많다. 그러나 모든 xi가 0인 명백한 해가 존재하므로, 이 연립방정식의 해는 무한히 많다. 그러므로 v→1, v→2, … , v→n+1는 linearly dependent이다.
이러한 이유로 basis의 vector의 개수는 매우 특별한 수라고 하겠다. 이 수를 vector space의 dimension이라고 부른다. 만약 basis의 vector의 수가 유한하다면 그 vector space를 finite dimensional vector space라고 부르고 유한하지 않다면 infinite dimensional vector space라고 부른다.
Basis에서 중요한 점은 basis 선택은 유일하지 않다는 점이다. 단지 임의로 위의 두 조건에 맞게 basis를 구성할 수 있다.
# Sum of Rank-1 Outer Products
그 장점이 무엇인가?
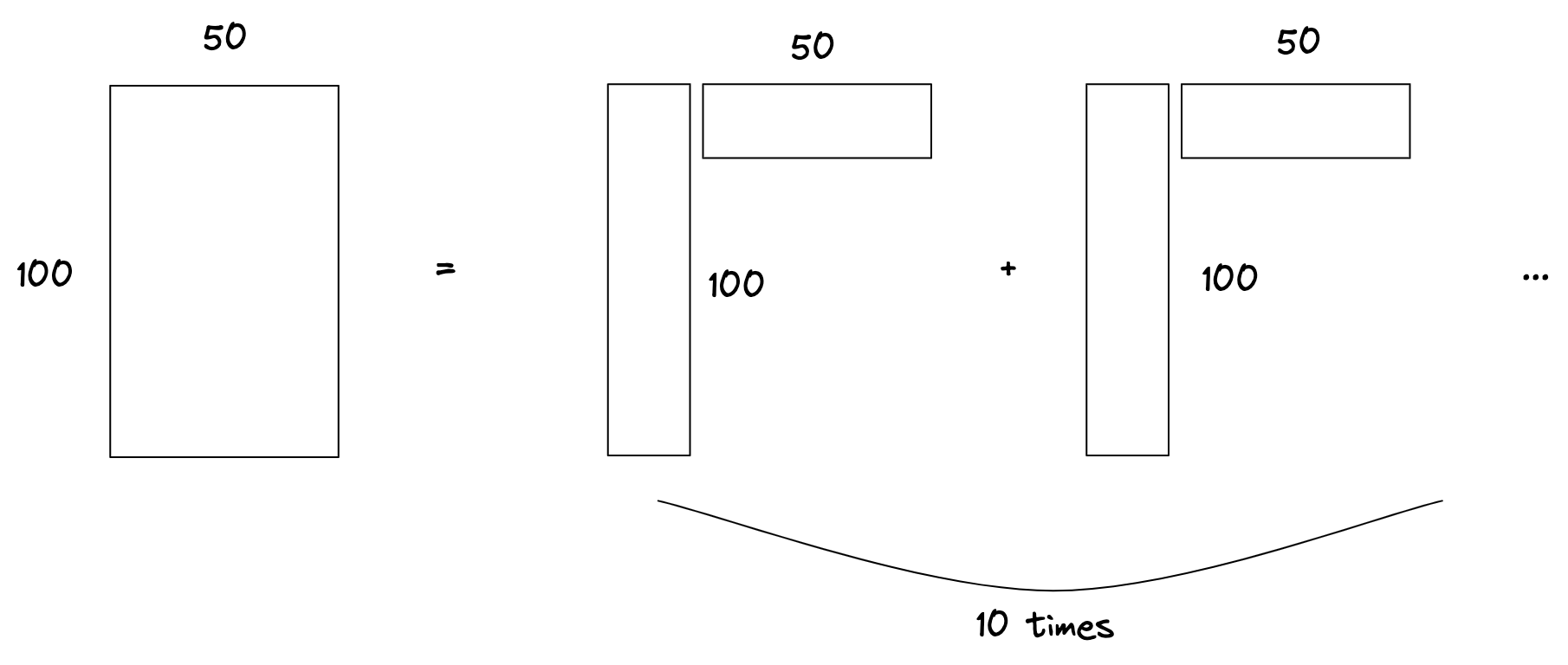
100_50개의 숫자를 단지 150_10개의 숫자로 표현할 수 있다. 정확하진 않지만, 근사적으로.